# 栈
# 概念
栈是一个线性结构,在计算机中是一个相当常见的数据结构。
栈的特点是只能在某一端添加或删除数据,遵循先进后出的原则:

# 实现
每种数据结构都可以用很多种方式来实现,其实可以把栈看成是数组的一个子集,所以这里使用数组来实现:
class Stack {
constructor() {
this.stack = []
}
push(item) {
this.stack.push(item)
}
pop() {
this.stack.pop()
}
peek() {
return this.stack[this.getCount() - 1]
}
getCount() {
return this.stack.length
}
isEmpty() {
return this.getCount() === 0
}
}
# 应用
# 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例一:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
示例 4:
输入:s = "([)]"
输出:false
示例 5:
输入:s = "{[]}"
输出:true
题意是匹配括号,可以通过栈的特性来完成这道题目:
/**
* 解法一
* 时间复杂度:O(n)
* 空间复杂度:O(n)
*/
var isValid = function (s) {
let stack = [];
for (var i = 0; i < s.length; i++) {
let c = s.charAt(i);
if (c === '(') {
// 遇左添右
stack.push(')');
} else if (c === '[') {
stack.push(']');
} else if (c === '{') {
stack.push('}');
} else if (c !== stack[stack.length - 1] || !stack.length) {
// 验证是否当前的右括号和栈顶一致(符合配对关系),验证是否此时的右括号是多余的(右多左少)
return fasle;
} else {
// 正常弹出栈顶元素,消左
stack.pop();
}
}
return !stack.length;
}
/**
* 解法二
* 时间复杂度:O(n)
* 空间复杂度:O(n)
*/
var isValid = function(s) {
let map = {
'(': -1,
')': 1,
'[': -2,
']': 2,
'{': -3,
'}': 3
};
let stack = [];
for (let i = 0; i < s.length; i++) {
if (map[s[i]] < 0) {
stack.push(s[i])
} else {
let last = stack.pop();
if (map[last] + map[s[i]] != 0) return false;
}
}
return stack.length > 0 ? false : true;
}
# 树
# 二叉树
# 概念
树拥有很多种结构,二叉树是树中最常用的结构,同时也是一个天然的递归结构。
二叉树拥有一个根节点,每个节点至多拥有两个子节点,分别为:左节点和右节点。树的最底部节点称之为叶节点,当一颗树的叶数量为满时,该树可以称之为满二叉树。
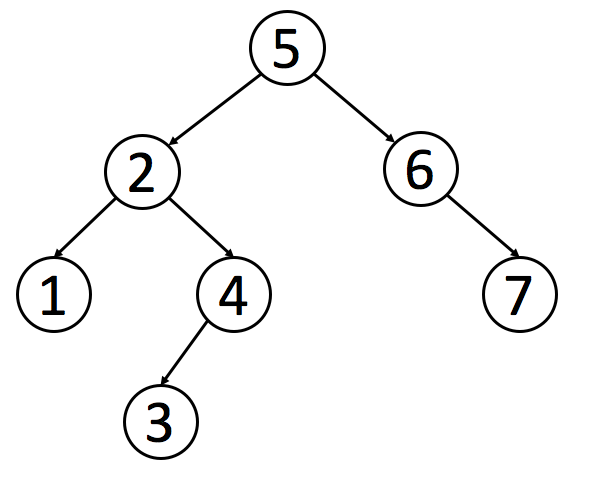
二叉搜索树:
二叉搜索树也是二叉树,拥有二叉树的特性。但是区别在于二分搜索树每个节点的值都比他的左子树的值大,比右子树的值小。
这种存储方式很适合于数据搜索。如下图所示,当需要查找 6 的时候,因为需要查找的值比根节点的值大,所以只需要在根节点的右子树上寻找,大大提高了搜索效率。

# 实现
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
/**
* 二叉搜索树
*/
class BST {
constructor() {
this.root = null;
this.size = 0;
}
getSize() {
return this.size;
}
isEmpty() {
return this.size === 0;
}
addNode(v) {
this.root = this._addChild(this.root, v);
}
// 添加节点时,需要比较添加的节点值和当前
// 节点值的大小
_addChild(node, v) {
if (!node) {
this.size++;
return new Node(v);
}
if (node.value > v) {
node.left = this._addChild(node.left, v);
} else if (node.value < v) {
node.right = this._addChild(node.right, v);
}
return node;
}
}
以上是最基本的二分搜索树实现,接下来实现树的遍历。
对于树的遍历来说,有三种遍历方法,分别是先序遍历、中序遍历、后序遍历。三种遍历的区别在于何时访问节点。在遍历树的过程中,每个节点都会遍历三次,分别是遍历到自己,遍历左子树和遍历右子树。如果需要实现先序遍历,那么只需要第一次遍历到节点时进行操作即可。
// 先序遍历可用于打印树的结构
// 先序遍历:根->左->右,先访问根节点,然后访问左节点,最后访问右节点。
preTraversal() {
this._pre(this.root);
}
_pre(node) {
if (node) {
console.log(node.value);
this._pre(node.left);
this._pre(node.right);
}
}
// 中序遍历可用于排序
// 对于 BST 来说,中序遍历可以实现一次遍历就得到有序的值
// 中序遍历:左->根->右,表示先访问左节点,然后访问根节点,最后访问右节点。
midTraversal() {
this._mid(this.root);
}
_mid(node) {
if (node) {
this._mid(node.left);
console.log(node.value);
this._mid(node.right);
}
}
// 后序遍历可用于先操作子节点再操作父节点的场景
// 后序遍历:左->右->根,表示先访问左节点,然后访问右节点,最后访问根节点。
backTraversal() {
this._back(this.root);
}
_back(node) {
if (node) {
this._back(node.left);
this._back(node.right);
console.log(node.value);
}
}
以上的这几种遍历都可以称之为深度遍历,对应的还有种遍历叫做广度遍历(也叫层序遍历),就是一层层地遍历树。对于广度遍历来说,我们需要利用 队列 结构来完成。
// 层序遍历:从上到下,同层节点从左到右
breadthTraversal() {
if (!this.root) return null;
let q = new Queue();
// 将根节点入队
q.enQueue(this.root);
// 循环判断队列是否为空,为空代表树遍历完毕
while (!q.isEmpty()) {
// 将队首出队,判断是否有左右子树
// 有的话,就先左后右入队
let n = q.deQueue();
console.log(n.value);
if (n.left) q.enQueue(n.left);
if (n.right) q.enQueue(n.right);
}
}
// 本质上是利用数组实现队列的「先入先出」原则
// 可简化下代码:
breadthTraversal() {
if (!this.root) return null;
let q = [];
q.push(this.root);
while(q.length) {
let n = q.pop();
console.log(n.value);
if (n.left) q.push(n.left);
if (n.right) q.push(n.right);
}
}
接下来先介绍如何在树中寻找最小值或最大数。因为二分搜索树的特性,所以最小值一定在根节点的最左边,最大值相反:
getMin() {
return this._getMin(this.root).value;
}
_getMin(node) {
if (!node.left) return node;
return this._getMin(node.left);
}
getMax() {
return this._getMax(this.root).value;
}
_getMax(node) {
if (!node.right) return node;
return this._getMin(node.right);
}
向上取整和向下取整,这两个操作是相反的,所以代码也是类似的,这里只介绍如何向下取整。既然是向下取整,那么根据二分搜索树的特性,值一定在根节点的左侧。只需要一直遍历左子树直到当前节点的值不再大于等于需要的值,然后判断节点是否还拥有右子树。如果有的话,继续上面的递归判断。
floor(v) {
let node = this._floor(this.root, v);
return node ? node.value : null;
}
_floor(node, v) {
if (!node) return null;
if (node.value === v) return node;
// 如果当前节点值还比需要的值大,就继续递归
if (node.value > v) {
return this._floor(node.left, v);
}
// 判断当前节点是否拥有右子树
let right = this._floor(node.right, v);
if (right) return right;
return node;
}
排名,这是用于获取给定值的排名或者排名第几的节点的值,这两个操作也是相反的,所以这个只介绍如何获取排名第几的节点的值。对于这个操作而言,我们需要略微的改造点代码,让每个节点拥有一个 size 属性。该属性表示该节点下有多少子节点(包含自身)。
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
// 修改代码
this.size = 1
}
}
class BST {
// ...
// 新增代码
_getSize(node) {
return node ? node.size : 0;
}
_addChild(node, v) {
if (!node) {
return new Node(v);
}
// 修改代码
node.size++;
if (node.value > v) {
node.left = this._addChild(node.left, v);
} else if (node.value < v) {
node.right = this._addChild(node.right, v);
}
return node;
}
select(k) {
let node = this._select(this.root, k);
return node ? node.value : null;
}
_select(node, k) {
if (!node) return null;
// 先获取左子树下有几个节点
let size = node.left ? node.left.size : 0;
// 判断 size 是否大于 k
// 如果大于 k,代表所需要的节点在左节点
if (size > k) return this._select(node.left, k);
// 如果小于 k,代表所需要的节点在右节点
// 注意这里需要重新计算 k,减去根节点除了右子树的节点数量
if (size < k) return this._select(node.right, k - size - 1);
return node;
}
}
接下来讲解的是二分搜索树中最难实现的部分:删除节点。因为对于删除节点来说,会存在以下几种情况:
- 需要删除的节点没有子树
- 需要删除的节点只有一条子树
- 需要删除的节点有左右两条树
对于前两种情况很好解决,但是第三种情况就有难度了,所以先来实现相对简单的操作:删除最小节点,对于删除最小节点来说,是不存在第三种情况的,删除最大节点操作是和删除最小节点相反的,所以这里也就不再赘述。
delectMin() {
this.root = this._delectMin(this.root);
console.log(this.root);
}
_delectMin(node) {
// 一直递归左子树
// 如果左子树为空,就判断节点是否拥有右子树
// 有右子树的话就把需要删除的节点替换为右子树
if ((node != null) & !node.left) return node.right;
node.left = this._delectMin(node.left);
// 最后需要重新维护下节点的 `size`
node.size = this._getSize(node.left) + this._getSize(node.right) + 1;
return node;
}
最后讲解的就是如何删除任意节点了。对于这个操作,T.Hibbard 在 1962 年提出了解决这个难题的办法,也就是如何解决第三种情况。
当遇到这种情况时,需要取出当前节点的后继节点(也就是当前节点右子树的最小节点)来替换需要删除的节点。然后将需要删除节点的左子树赋值给后继结点,右子树删除后继结点后赋值给他。
你如果对于这个解决办法有疑问的话,可以这样考虑。因为二分搜索树的特性,父节点一定比所有左子节点大,比所有右子节点小。那么当需要删除父节点时,势必需要拿出一个比父节点大的节点来替换父节点。这个节点肯定不存在于左子树,必然存在于右子树。然后又需要保持父节点都是比右子节点小的,那么就可以取出右子树中最小的那个节点来替换父节点。
delect(v) {
this.root = this._delect(this.root, v);
}
_delect(node, v) {
if (!node) return null;
// 寻找的节点比当前节点小,去左子树找
if (node.value < v) {
node.right = this._delect(node.right, v);
} else if (node.value > v) {
// 寻找的节点比当前节点大,去右子树找
node.left = this._delect(node.left, v);
} else {
// 进入这个条件说明已经找到节点
// 先判断节点是否拥有拥有左右子树中的一个
// 是的话,将子树返回出去,这里和 `_delectMin` 的操作一样
if (!node.left) return node.right;
if (!node.right) return node.left;
// 进入这里,代表节点拥有左右子树
// 先取出当前节点的后继结点,也就是取当前节点右子树的最小值
let min = this._getMin(node.right);
// 取出最小值后,删除最小值
// 然后把删除节点后的子树赋值给最小值节点
min.right = this._delectMin(node.right);
// 左子树不动
min.left = node.left;
node = min;
}
// 维护 size
node.size = this._getSize(node.left) + this._getSize(node.right) + 1;
return node;
}
# AVL 树
# 概念
二分搜索树实际在业务中是受到限制的,因为并不是严格的 O(㏒n),在极端情况下会退化成链表,比如加入一组升序的数字就会造成这种情况:
5
\
7
\
8
\
10
\
15
AVL 树改进了二分搜索树,在 AVL 树中任意节点的左右子树的高度差都不大于 1,这样保证了时间复杂度是严格的 O(㏒n)。基于此,对 AVL 树增加或删除节点时可能需要旋转树来达到高度的平衡。
# 实现
因为 AVL 树是改进了二分搜索树,所以部分代码是于二分搜索树重复的,对于重复内容不作再次解析。
对于 AVL 树来说,添加节点会有四种情况:
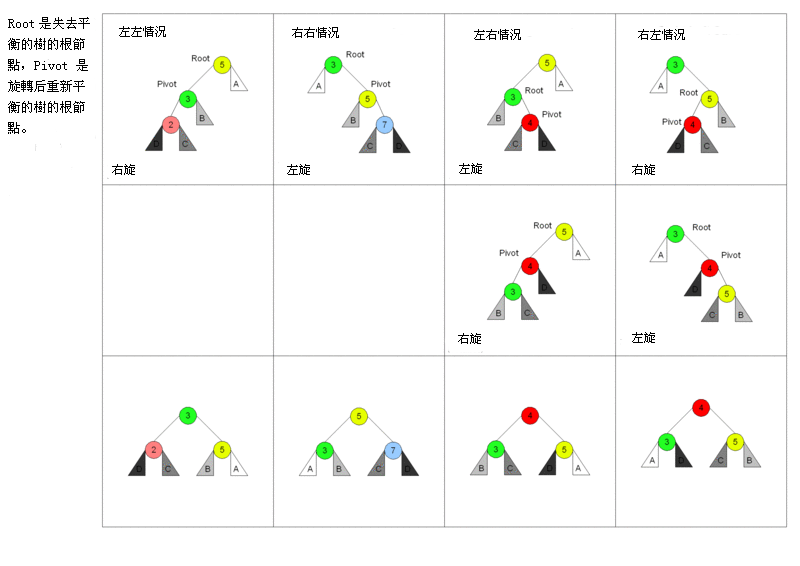
对于左左情况来说,新增加的节点位于节点 2 的左侧,这时树已经不平衡,需要旋转。因为搜索树的特性,节点比左节点大,比右节点小,所以旋转以后也要实现这个特性。
旋转之前:new < 2 < C < 3 < B < 5 < A,右旋之后节点 3 为根节点,这时候需要将节点 3 的右节点加到节点 5 的左边,最后还需要更新节点的高度。
对于右右情况来说,相反于左左情况,所以不再赘述。
对于左右情况来说,新增加的节点位于节点 4 的右侧。对于这种情况,需要通过两次旋转来达到目的。
首先对节点的左节点左旋,这时树满足左左的情况,再对节点进行一次右旋就可以达到目的。
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
this.height = 1
}
}
class AVL {
constructor() {
this.root = null;
}
addNode(v) {
this.root = this._addChild(this.root, v);
}
_addChild(node, v) {
if (!node) {
return new Node(v);
}
if (node.value > v) {
node.left = this._addChild(node.left, v);
} else if (node.value < v) {
node.right = this._addChild(node.right, v);
} else {
node.value = v
}
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right));
let factor = this._getBalanceFactor(node);
// 当需要右旋时,根节点的左树一定比右树高度高
if (factor > 1 && this._getBalanceFactor(node.left) >= 0) {
return this._rightRotate(node);
}
// 当需要左旋时,根节点的左树一定比右树高度矮
if (factor < -1 && this._getBalanceFactor(node.right) <= 0) {
return this._leftRotate(node);
}
// 左右情况
// 节点的左树比右树高,且节点的左树的右树比节点的左树的左树高
if (factor > 1 && this._getBalanceFactor(node.left) < 0) {
node.left = this._leftRotate(node.left);
return this._rightRotate(node);
}
// 右左情况
// 节点的左树比右树矮,且节点的右树的右树比节点的右树的左树矮
if (factor < -1 && this._getBalanceFactor(node.right) > 0) {
node.right = this._rightRotate(node.right);
return this._leftRotate(node);
}
return node;
}
_getHeight(node) {
if (!node) return 0;
return node.height;
}
_getBalanceFactor(node) {
return this._getHeight(node.left) - this._getHeight(node.right);
}
// 节点右旋
// 5 2
// / \ / \
// 2 6 ==> 1 5
// / \ / / \
// 1 3 new 3 6
// /
// new
_rightRotate(node) {
// 旋转后新根节点
let newRoot = node.left;
// 需要移动的节点
let moveNode = newRoot.right;
// 节点 2 的右节点改为节点 5
newRoot.right = node;
// 节点 5 左节点改为节点 3
node.left = moveNode;
// 更新树的高度
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right));
newRoot.height =
1 +
Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right));
return newRoot;
}
// 节点左旋
// 4 6
// / \ / \
// 2 6 ==> 4 7
// / \ / \ \
// 5 7 2 5 new
// \
// new
_leftRotate(node) {
// 旋转后新根节点
let newRoot = node.right;
// 需要移动的节点
let moveNode = newRoot.left;
// 节点 6 的左节点改为节点 4
newRoot.left = node;
// 节点 4 右节点改为节点 5
node.right = moveNode;
// 更新树的高度
node.height =
1 + Math.max(this._getHeight(node.left), this._getHeight(node.right));
newRoot.height =
1 +
Math.max(this._getHeight(newRoot.left), this._getHeight(newRoot.right));
return newRoot
}
}
# 堆
# 概念
堆通常是一个可以被看做一棵树的数组对象。
堆的实现通过构造二叉堆,实为二叉树的一种。这种数据结构具有以下性质:
- 任意节点小于(或大于)它的所有子节点
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层从左到右填入。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
优先队列也完全可以用堆来实现,操作是一模一样的。
# 实现大根堆
堆的每个节点的左边子节点索引是 i * 2 + 1,右边是 i * 2 + 2,父节点是 (i - 1) /2。
堆有两个核心的操作,分别是 shiftUp 和 shiftDown。前者用于添加元素,后者用于删除根节点:
shiftUp: 核心思路是一路将节点与父节点对比大小,如果比父节点大,就和父节点交换位置shiftDown: 核心思路是先将根节点和末尾交换位置,然后移除末尾元素。接下来循环判断父节点和两个子节点的大小,如果子节点大,就把最大的子节点和父节点交换
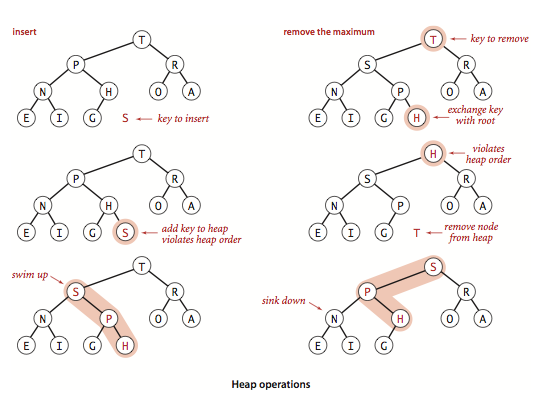
class MaxHeap {
constructor() {
this.heap = [];
}
size() {
return this.heap.length;
}
empty() {
return this.size() == 0;
}
add(item) {
this.heap.push(item);
this._shiftUp(this.size() - 1);
}
removeMax() {
this._shiftDown(0);
}
getParentIndex(k) {
return parseInt((k - 1) / 2);
}
getLeftIndex(k) {
return k * 2 + 1;
}
_shiftUp(k) {
// 如果当前节点比父节点大,就交换
while (this.heap[k] > this.heap[this.getParentIndex(k)]) {
this._swap(k, this.getParentIndex(k));
// 将索引变成父节点
k = this.getParentIndex(k);
}
}
_shiftDown(k) {
// 交换首位并删除末尾
this._swap(k, this.size() - 1)
this.heap.splice(this.size() - 1, 1)
// 判断节点是否有左孩子,因为二叉堆的特性,有右必有左
while (this.getLeftIndex(k) < this.size()) {
let j = this.getLeftIndex(k);
// 判断是否有右孩子,并且右孩子是否大于左孩子
if (j + 1 < this.size() && this.heap[j + 1] > this.heap[j]) j++;
// 判断父节点是否已经比子节点都大
if (this.heap[k] >= this.heap[j]) break;
this._swap(k, j);
k = j;
}
}
_swap(left, right) {
let rightValue = this.heap[right];
this.heap[right] = this.heap[left];
this.heap[left] = rightValue;
}
}
# Trie
# 概念
在计算机科学,Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。
简单点来说,这个结构的作用大多是为了方便搜索字符串,该树有以下几个特点:
- 根节点代表空字符串,每个节点都有 N(假如搜索英文字符,就有 26 条)条链接,每条链接代表一个字符
- 节点不存储字符,只有路径才存储,这点和其他的树结构不同
- 从根节点开始到任意一个节点,将沿途经过的字符连接起来就是该节点对应的字符串
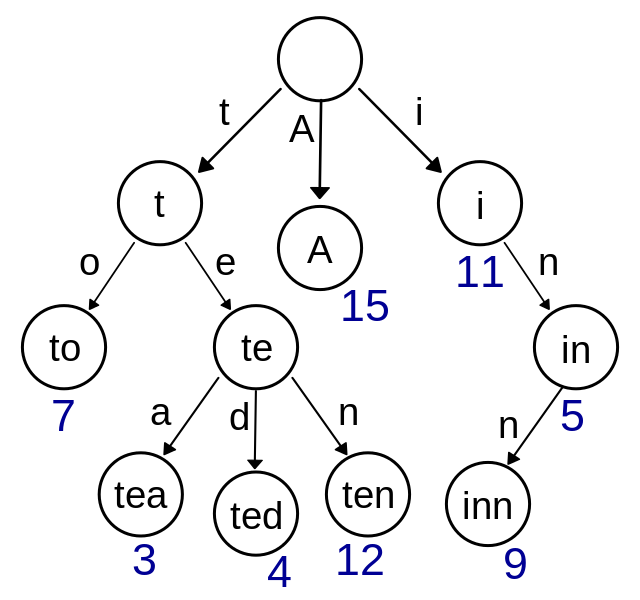
# 实现
总得来说 Trie 的实现相比别的树结构来说简单的很多,实现就以搜索英文字符为例:
class TrieNode {
constructor() {
// 代表每个字符经过节点的次数
this.path = 0;
// 代表到该节点的字符串有几个
this.end = 0;
// 链接
this.next = new Array(26).fill(null);
}
}
class Trie {
constructor() {
// 根节点,代表空字符
this.root = new TrieNode();
}
// 插入字符串
insert(str) {
if (!str) return;
let node = this.root;
for (let i = 0; i < str.length; i++) {
// 获得字符先对应的索引
let index = str[i].charCodeAt() - 'a'.charCodeAt();
// 如果索引对应没有值,就创建
if (!node.next[index]) {
node.next[index] = new TrieNode();
}
node.path += 1;
node = node.next[index];
}
node.end += 1;
}
// 搜索字符串出现的次数
search(str) {
if (!str) return;
let node = this.root;
for (let i = 0; i < str.length; i++) {
let index = str[i].charCodeAt() - 'a'.charCodeAt();
// 如果索引对应没有值,代表没有需要搜素的字符串
if (!node.next[index]) {
return 0;
}
node = node.next[index];
}
return node.end;
}
// 删除字符串
delete(str) {
if (!this.search(str)) return;
let node = this.root;
for (let i = 0; i < str.length; i++) {
let index = str[i].charCodeAt() - 'a'.charCodeAt();
// 如果索引对应的节点的 Path 为 0,代表经过该节点的字符串
// 已经一个,直接删除即可
if (--node.next[index].path == 0) {
node.next[index] = null;
return;
}
node = node.next[index];
}
node.end -= 1;
}
}
# 队列
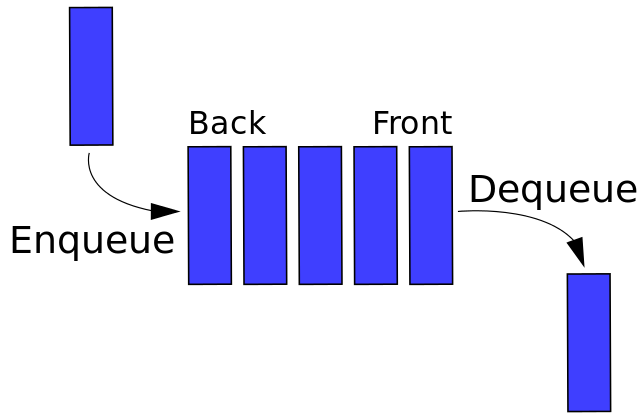
# 概念
队列一个线性结构,特点是在某一端添加数据,在另一端删除数据,遵循先进先出的原则。
# 实现
这里会讲解两种实现队列的方式,分别是单链队列和循环队列。
# 单链队列
class Queue {
constructor() {
this.queue = [];
}
enQueue(item) {
this.queue.push(item);
}
deQueue() {
return this.queue.shift();
}
getHeader() {
return this.queue[0];
}
getLength() {
return this.queue.length;
}
isEmpty() {
return this.getLength() === 0;
}
}
因为单链队列在出队操作的时候需要 O(n) 的时间复杂度,所以引入了循环队列。循环队列的出队操作平均是 O(1) 的时间复杂度。
# 循环队列
class SqQueue {
constructor(length) {
this.queue = new Array(length + 1);
// 队头
this.first = 0;
// 队尾
this.last = 0;
// 当前队列大小
this.size = 0;
}
enQueue(item) {
// 判断队尾 + 1 是否为队头
// 如果是就代表需要扩容数组
// % this.queue.length 是为了防止数组越界
if (this.first === (this.last + 1) % this.queue.length) {
this.resize(this.getLength() * 2 + 1);
}
this.queue[this.last] = item;
this.size++;
this.last = (this.last + 1) % this.queue.length;
}
deQueue() {
if (this.isEmpty()) {
throw Error('Queue is empty');
}
let r = this.queue[this.first];
this.queue[this.first] = null;
this.first = (this.first + 1) % this.queue.length;
this.size--;
// 判断当前队列大小是否过小
// 为了保证不浪费空间,在队列空间等于总长度四分之一时
// 且不为 2 时缩小总长度为当前的一半
if (this.size === this.getLength() / 4 && this.getLength() / 2 !== 0) {
this.resize(this.getLength() / 2);
}
return r;
}
getHeader() {
if (this.isEmpty()) {
throw Error('Queue is empty');
}
return this.queue[this.first];
}
getLength() {
return this.queue.length - 1;
}
isEmpty() {
return this.first === this.last;
}
resize(length) {
let q = new Array(length);
for (let i = 0; i < length; i++) {
q[i] = this.queue[(i + this.first) % this.queue.length];
}
this.queue = q;
this.first = 0;
this.last = this.size;
}
}
# 链表
# 概念
链表是一个线性结构,同时也是一个天然的递归结构。链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。

# 实现
# 单向链表
class Node {
constructor(v, next) {
this.value = v;
this.next = next;
}
}
class LinkList {
constructor() {
// 链表长度
this.size = 0;
// 虚拟头部
this.dummyNode = new Node(null, null);
}
find(header, index, currentIndex) {
if (index === currentIndex) return header;
return this.find(header.next, index, currentIndex + 1);
}
addNode(v, index) {
this.checkIndex(index);
// 当往链表末尾插入时,prev.next 为空
// 其他情况时,因为要插入节点,所以插入的节点
// 的 next 应该是 prev.next
// 然后设置 prev.next 为插入的节点
let prev = this.find(this.dummyNode, index, 0);
prev.next = new Node(v, prev.next);
this.size++;
return prev.next;
}
insertNode(v, index) {
return this.addNode(v, index);
}
addToFirst(v) {
return this.addNode(v, 0);
}
addToLast(v) {
return this.addNode(v, this.size);
}
removeNode(index, isLast) {
this.checkIndex(index);
index = isLast ? index - 1 : index;
let prev = this.find(this.dummyNode, index, 0);
let node = prev.next;
prev.next = node.next;
node.next = null;
this.size--;
return node;
}
removeFirstNode() {
return this.removeNode(0);
}
removeLastNode() {
return this.removeNode(this.size, true);
}
checkIndex(index) {
if (index < 0 || index > this.size) throw Error('Index error');
}
getNode(index) {
this.checkIndex(index);
if (this.isEmpty()) return;
return this.find(this.dummyNode, index, 0).next;
}
isEmpty() {
return this.size === 0;
}
getSize() {
return this.size;
}
}
# 反转单向链表
class LinkList {
// ...
reverseList() {
let header = this.dummyNode.next;
// 判断变量边界
if (!header || !header.next) return;
// 初始设置为空,因为第一个节点反转后就是尾部,尾部节点指向 null
let pre = null;
let current = header;
let next;
// 判断当前节点是否为空
// 不为空就先获取当前节点的下一节点
// 然后把当前节点的 next 设为上一个节点
// 然后把 current 设为下一个节点,pre 设为当前节点
while (current) {
next = current.next;
current.next = pre;
pre = current;
current = next;
}
this.dummyNode.next = pre;
}
// ...
}
# 链表中环的检测
class LinkList {
// ...
hasCycle() {
let node = this.root;
while (node) {
if (node.value === 'cycleFlag') return true;
node.value = 'cycleFlag';
node = node.next;
}
return false;
}
// ...
}
# 并查集
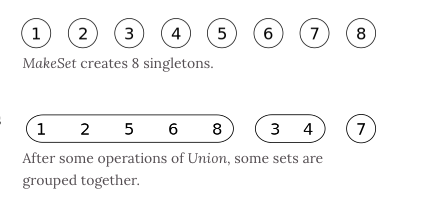
# 概念
并查集是一种特殊的树结构,用于处理一些不交集的合并及查询问题。该结构中每个节点都有一个父节点,如果只有当前一个节点,那么该节点的父节点指向自己。
这个结构中有两个重要的操作,分别是:
- Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合。
# 实现
class DisjointSet {
// 初始化样本
constructor(count) {
// 初始化时,每个节点的父节点都是自己
this.parent = new Array(count);
// 用于记录树的深度,优化搜索复杂度
this.rank = new Array(count);
for (let i = 0; i < count; i++) {
this.parent[i] = i;
this.rank[i] = 1;
}
}
find(p) {
// 寻找当前节点的父节点是否为自己,不是的话表示还没找到
// 开始进行路径压缩优化
// 假设当前节点父节点为 A
// 将当前节点挂载到 A 节点的父节点上,达到压缩深度的目的
while (p != this.parent[p]) {
this.parent[p] = this.parent[this.parent[p]];
p = this.parent[p];
}
return p;
}
isConnected(p, q) {
return this.find(p) === this.find(q);
}
// 合并
union(p, q) {
// 找到两个数字的父节点
let i = this.find(p);
let j = this.find(q);
if (i === j) return;
// 判断两棵树的深度,深度小的加到深度大的树下面
// 如果两棵树深度相等,那就无所谓怎么加
if (this.rank[i] < this.rank[j]) {
this.parent[i] = j;
} else if (this.rank[i] > this.rank[j]) {
this.parent[j] = i;
} else {
this.parent[i] = j;
this.rank[j] += 1;
}
}
}
